マヤのカレンダー

●260日暦（神聖暦：マヤ語でツォルキン）
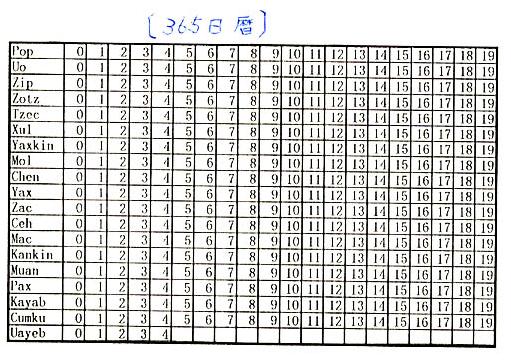
　日をあらわす20の文字の文字と１〜13の文字を組み合わせて表現する。日を表す20の文字の読み方は、次の通り。
　　　1)イミシュ(Imix)
　　　2)イク(Ik)
　　　3) アクバル(Akbal)
　　　4) カン(Kan)
　　　5) チクチャン(Chicchan)
　　　6) キミ(Cimi)
　　　7) マニク(Manik)
　　　8) ラマト(Lamat)
　　　9) ムルク(Mulc)
　　　10) オク(Oc)		 11) チュエン(Chuen)
12) エブ(Eb)
13) ベン(Ben)
14) イシュ(Ix)
15) メン(Men)
16) キブ(Cib)
17) カバン(Caban)
18) エツナッブ(Etz'nab)
19) カワック(Cauac)
20)アハウ(Ahau)
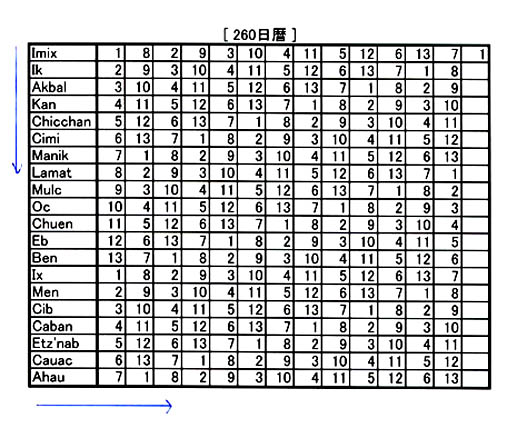
　ツォルキンの第1日目は、「１イミシュ」と呼ばれ、第２日目は「２イク」、第３日目は「３アクバル」と続き20と13の最小公倍数である260が経過すると「１イミシュ」に戻る（図6-3-1、参照）。この暦は、儀式や占いに使用された。マヤ人は、日と数は神聖なものと考えていたためその組み合わせが幸運や強運をもたらすと信じていた。
図6-3-1
↓


●365日暦(太陽暦）
　マヤには、儀式暦の他に、360日+５日を1年とする太陽暦もあった。この太陽暦は、1ヶ月が20日(0 〜19)からなる月が18ヶ月（360日）とワァイェブと呼ばれる５日だけの短い月が加えられ365日と計算していた。365日暦では、第1日目が「0ポップ」、第2日目が「1ポップ」・・ポップの月の最後の日が「19 ポップ」となる。365日暦は、年中の農作業や定期的に開催される祭りの日を決めるために用いられたと考えられている。
　18ヶ月の月の名前は次にに示すとおりである。
　　　1) ポプ(Pop)
　　　2) ウォ(Uo)
　　　3) シップ(Zip)
　　　4) ソッツ(Zotz)
　　　5) セック(Tzec)
　　　6) シュル(Xul)
　　　7) ヤシュキン(Yaxkin)
　　　8) モル(Mol)
　　　9) チェン(Chen)
　　　10) ヤシュ(Yax)		 11) サック(Zac)
12) ケフ(Ceh)
13) マック(Mac)
14) カンキン(Kankin)
15) ムアン(Muan)
16) パシュ(Pax)
17) カヤッブ(Kayab)
18) クムク(Cumku)
19) ワヤッブ(Uayeb)
図6-2-2
↓

●長期暦
　長期暦は、碑文の冒頭に置かれる日付で、普通５つの部分（バクトゥン、カトゥン、トゥン、ウィナル、キン）で構成される。これは、暦の起点となる日から碑文に記された時点までに経過した日数を計算して得られる暦である。西暦の起点は、キリストが誕生した日であるが、マヤ人が起点として撰んだ日は、13.0.0.0.0　４アハウ　８クムクである（読み方：13バクトゥン、0カトゥン、0トゥン、0ウィナル、0キン、４アハウ、８クムク）。この日が西暦のいつにあたるかについては諸説があるが、現在もっとも受け入れられているのは紀元前 3114年8月11日（8月2日の説もある）である。
暦位取り
　キン（Kin） ：0〜19
　ウィナル（１Uinal＝20キン（20日））
　トゥン（１Tun＝：18ウィナル（360日、約1年）
　カトゥン（１Katun＝20トゥン（7200日、約20年)
　バクトゥン（１Baktun＝20カトゥン（144000日、約400年）
全体として20進法で数えられるがトゥンの位は、 18ウィナルで位が上がる。

●ライデン・プレート
　グァテマラの東海岸で発見され、現在オランダのライデン博物館にあるヒスイの板（通称：ラインデン・プレート）を見てみよう。表には、着飾った人物像、裏には日付が彫ってある（図6-3-3）。
　最初の文字（ISIG）は、長期暦の最初に出現する文字で、現在の「西暦」等と同じ意味がある文字である。次に、８・14・３・１・12（８バクトゥン、14カトゥン、３トゥン、１ウィナル、12キン）と続き、その後に260日暦の１エブ、365日暦の０ヤシュキンの日付が見られる。数字の右側の単位は、それぞれの位取りを表している。それでは、位取りに従って計算してみよう。
　８バクトゥン ：８×144000 ＝1,152,000日
　14カトゥン ：14×7200　 ＝ 100,800日
　３トゥン ：３×360　 ＝ 1,080日
　１キン ：1×20 ＝ 20日
　12ウィナル　 ：12×１ ＝ 12日
　合計 　1,152,000日
　これは、紀元前3114年8月11日から1,152,000日経過した日を示す。これは、西暦であらわすと、紀元後 320年に相当する。
図6-3-3
↓